|
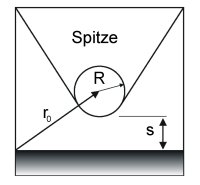
Im wesentlichen entsprechen die Betriebsmodi des STM denen des AFM. Leider ist die Interpretation des Messsignals nicht so einfach, wie es die verwendeten Prinzipien vermuten lassen. Um überhaupt in der Lage zu sein, die erhaltenen Bilder interpretieren zu können, muss man sich vergegenwärtigen, wie sich der gemessene Strom zusammensetzt. So ist zunächst notwendig, die einzelnen Beiträge einer bestimmten Probe sowie der Spitze an sich zum Tunnelstrom zu berechnen. Tersoff und Hamann (1983) wählten hierzu als Ansatz ein sehr einfaches Modell einer lokal sphärischen Spitze. Der Tunnelstrom kann dabei
folgendermaßen angenähert werden: |
 |
|
An obiger Gleichung erkennt man nun das eigentliche Problem bei der Interpretation der mit dem STM aufgenommenen Bilder. Der Tunnelstrom hängt sowohl von der lokalen Zustandsdichte (LDOS) der Spitze als auch von der LDOS der Oberfläche am Fermi-Niveau ab. Dabei kann die LDOS der Spitze normalerweise als konstant angenommen werden, da die meisten Spitzenmaterialien Metalle sind. Somit entspricht ein größeres z-Signal aber nicht unbedingt einer höherer Stelle der Oberfläche, wenn man eine Probe hat, die sich aus Materialien mit unterschiedlicher LDOS zusammensetzt. Aus dem Modell von Tersoff und Hamann geht auch eine wichtige Eigenschaft des Tunnelstroms hervor, nämlich die exponentielle Abhängigkeit vom Abstand zwischen Spitze und Probe. Dies folgt aus der Tatsache, dass s-Wellen exponentiell in z-Richtung von der Oberfläche zum Vakuum hin abfallen. Hierauf beruht das große Auflösungsvermögen eines Rastertunnelmikroskops. |

